Descriptive statistics

Quantitative and graphical techniques for summarizing data

Today’s agenda

Quick review of Lab 1
[lecture] frequency distributions, measures of spread and center, measures of association
[lab] descriptive statistics and simple graphics in R

Last time

Data semantics

Data are a collection of measurements taken on a sample of study units:

measured attributes are called variables
per-unit measurements are called observations

Variables are classified by their values:

categorical data: ordinal (ordered) or nominal (unordered) categories
numeric data: continuous (no ‘gaps’) or discrete (‘gaps’) numbers

Data structures

Observations of many variables are stored as data frames:

# 3 observations of age and sex
head(subjects, 3)

  subject.id age sex
1         11  24   m
2          2  31   m
3         31  17   f

Observations of a single variable are stored as vectors:

# extract age variable
ages <- subjects$age
ages

[1] 24 31 17

Dataset: FAMuSS study

Observational study of 595 individuals comparing change in arm strength before and after resistance training between genotypes for a region of interest on the ACTN3 gene.

Pescatello, L. S., et al. (2013). Highlights from the functional single nucleotide polymorphisms associated with human muscle size and strength or FAMuSS study. BioMed research international.

Example data rows
ndrm.ch	drm.ch	sex	age	race	height	weight	genotype	bmi
40	40	Female	27	Caucasian	65	199	CC	33.11
25	0	Male	36	Caucasian	71.7	189	CT	25.84
40	0	Female	24	Caucasian	65	134	CT	22.3
125	0	Female	40	Caucasian	68	171	CT	26

Descriptive statistics

Descriptive statistics refers to analysis of sample characteristics using summary statistics (functions of data) and/or graphics.

For example:

genotype	avg.change.strength	n.obs
TT	58.08	161
CT	53.25	261
CC	48.89	173

We call these descriptions and not inferences because they describe the sample:

Among study participants, those with genotype TT (n = 161) had the greatest average change in nondominant arm strength (58.08%).

The appropriate type of data summary depends on the variable type(s)!

Categorical frequency distributions

For categorical variables, the frequency distribution is simply an observation count by category. For example:

Raw data
participant.id	genotype
494	TT
510	TT
216	CT
19	TT
278	CT
86	TT

Frequency distribution
CC	CT	TT
173	261	161

Numeric frequency distributions

Frequency distributions of numeric variables are observation counts by “bins”: small intervals of a fixed width.

A plot of a numeric frequency distribution is called a histogram.

Data table
participant.id	bmi
194	22.3
141	20.76
313	23.48
522	29.29
504	42.28
273	20.34

Frequency distribution
(10,20]	(20,30]	(30,40]	(40,50]
69	461	58	7

Histograms and binning

Binning has a big effect on the visual impression. Which one captures the shape best?

Shapes

For numeric variables, the histogram reveals the shape of the distribution:

symmetric if it shows left-right symmetry about a central value
skewed if it stretches farther in one direction from a central value

Modes

Histograms also reveal the number of modes or local peaks of frequency distributions.

uniform if there are zero peaks
unimodal if there is one peak
bimodal if there are two peaks
multimodal if there are two or more peaks

Your turn: characterizing distributions

Consider four variables from the FAMuSS study. Describe the shape and modes.

Your turn: characterizing distributions

Here are some made-up data. Describe the shape and modes.

Common statistics as measures

Most common statistics measure a particular feature of the frequency distribution, typically either location/center or spread/variability.

Measures of center:

mean
median
mode

Measures of location:

percentiles/quantiles

Measures of spread:

range (min and max)
interquartile range
variance
standard deviation

The most appropriate choice of statistic(s) depends on the shape of the frequency distribution.

Measures of center

There are three common measures of center, each of which corresponds to a slightly different meaning of “typical”:

Measure	Definition
Mode	Most frequent value
Mean	Average value
Median	Middle value

Suppose your data consisted of the following observations of age in years:

19, 19, 21, 25 and 31

the mode or most frequent value is 19
the median or middle value is 21
the mean or average value is \(\frac{19 + 19 + 21 + 25 + 31}{5}\) = 23

Comparing measures of center

Each statistic is a little different, but often they roughly agree; for example, all are between 20 and 25, which seems to capture the typical BMI well enough.

The less symmetric the distribution, the less these measures agree.

Robustness to skew

The mean is more sensitive than the median to skewness:

Comparing means and medians captures information about skewness present since:

right skew: mean \(>\) median
left skew: mean \(<\) median
symmetry: mean \(\approx\) median

For skewed distributions, the median is a more robust measure of center.

Percentiles

A percentile is a threshold value that divides the observations into specific percentages.

Percentiles are defined by the percentage of data below the threshold, for example:

20th percentile: value exceeding exactly 20% of observations
60th percentile: value exceeding exactly 60% of observations

Sample percentiles are not unique!

age	19	20	21	25	31
rank	1	2	3	4	5

Any number between 19 and 20 is a 20th percentile since it would satisfy:

20% below (19)
80% above (20, 21, 25, 31)

Usually, pick the midpoint: 19.5.

Cumulative frequency distribution

The cumulative frequency distribution is a data summary showing percentiles. Think of it as percentile (y) against value (x).

Interpretation of some specific values:

about 40% of the subjects are 20 or younger
about 80% of the subjects are 24 or younger

Your turn:

Roughly what percentage of subjects are 22 or younger?
About what age is the 10th percentile?

Common percentiles

The five-number summary is a collection of five percentiles that succinctly describe the frequency distribution:

Statistic name	Meaning
minimum	0th percentile
first quartile	25th percentile
median	50th percentile
third quartile	75th percentile
maximum	100th percentile

Boxplots provide a graphical display of the five-number summary.

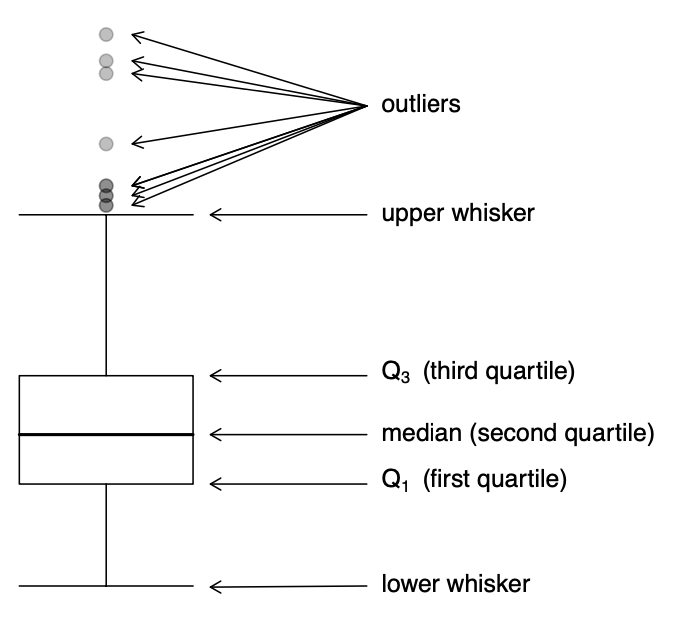
Boxplots vs. histograms

Notice how the two displays align, and also how they differ. The histogram shows shape in greater detail, but the boxplot is much more compact.

Measures of spread

The spread of observations refers to how concentrated or diffuse the values are.

Two ways to understand and measure spread:

ranges of values capturing much of the distribution
deviations of values from a central value

Range-based measures of spread

A simple way to understand and measure spread is based on ranges. Consider more ages, sorted and ranked:

age	16	18	19	20	21	22	25	26	28	29	30	34
rank	1	2	3	4	5	6	7	8	9	10	11	12

The range is the minimum and maximum values: \[\text{range} = (\text{min}, \text{max}) = (16, 34)\]
The interquartile range (IQR) is the difference [75th percentile] - [25th percentile] \[\text{IQR} = 29 - 19 = 10\]

Deviation-based measures of spread

Another way is based on deviations from a central value. Continuing the example, the mean age is is 24. The deviations of each observation from the mean are:

age	16	18	19	20	21	22	25	26	28	29	30	34
deviation	-8	-6	-5	-4	-3	-2	1	2	4	5	6	10

The variance is the average squared deviation from the mean (but divided by one less than the sample size): \[\frac{(-8)^2 + (-6)^2 + (-5)^2 + (-4)^2 + (-3)^2 + (-2)^2 + (1)^2 + (2)^2 + (4)^2 + (5)^2 + (6)^2 + (10)^2}{12 - 1}\]

In mathematical notation: \[S^2_x = \frac{1}{n - 1}\sum_{i = 1}^n (x_i - \bar{x})^2\]

Deviation-based measures of spread

Another way is based on deviations from a central value. Continuing the example, the mean age is is 24. The deviations of each observation from the mean are:

age	16	18	19	20	21	22	25	26	28	29	30	34
deviation	-8	-6	-5	-4	-3	-2	1	2	4	5	6	10

The standard deviation is the square root of the variance: \[\sqrt{\frac{(-8)^2 + (-6)^2 + (-5)^2 + (-4)^2 + (-3)^2 + (-2)^2 + (1)^2 + (2)^2 + (4)^2 + (5)^2 + (6)^2 + (10)^2}{12 - 1}}\]

In mathematical notation: \[S^2_y = \sqrt{\frac{1}{n - 1}\sum_{i = 1}^n (x_i - \bar{x})^2}\]

Interpretations

Listed from largest to smallest, here are each of the measures of spread for the 12 ages:

min	max	iqr	variance	st.dev	avg.dev
16	34	8.5	30.55	5.527	4.667

The interpretations differ between these statistics:

[range] all of the participants are between 16 and 34 years old
[IQR] the middle 50% of participants are within 8.5 years of age of each other
[variance] participants’ ages vary by an average of 30.55 squared years
[standard deviation] participants’ ages vary by an average of 5.53 years

Robustness to outliers

Percentile-based measures of location and spread are less sensitive to outliers

Consider adding an observation of 94 to our 12 ages. (This is called an outlier.)

# append an outlier
ages_add <- c(ages, 94)

# IQR
c(original = IQR(ages), with.outlier = IQR(ages_add))

    original with.outlier 
         8.5          9.0

# SD
c(original = sd(ages), with.outlier = sd(ages_add))

    original with.outlier 
    5.526794    20.122701

The effect of this outlier on each statistic is:

IQR increases by 5.88%
SD increases by 264.09%

In the presence of outliers, IQR is a more robust measure of spread.

Choosing appropriate measures

To determine which measures of spread and center to use, simply visualize the distribution and check for skewness and outliers.

strong skew or large outliers: prefer median/IQR to mean/SD
when in doubt, compute and compare

For example, which summary statistics are best to use below?

Next time: foundations for inference

How much would sample statistics change if we collected new (or different) data?

Assuming data come from random samples, we can answer this!

use sample statistics as point estimates of population statistics
quantify sampling variability: how much estimates change from sample to sample
construct interval estimates that capture the population statistic with high probability

Next time we’ll do this with the sample mean.