STAT218 - Inference in regression

Today’s agenda

[lecture] inference for the SLR model
[lab] predicting brain size

From last time

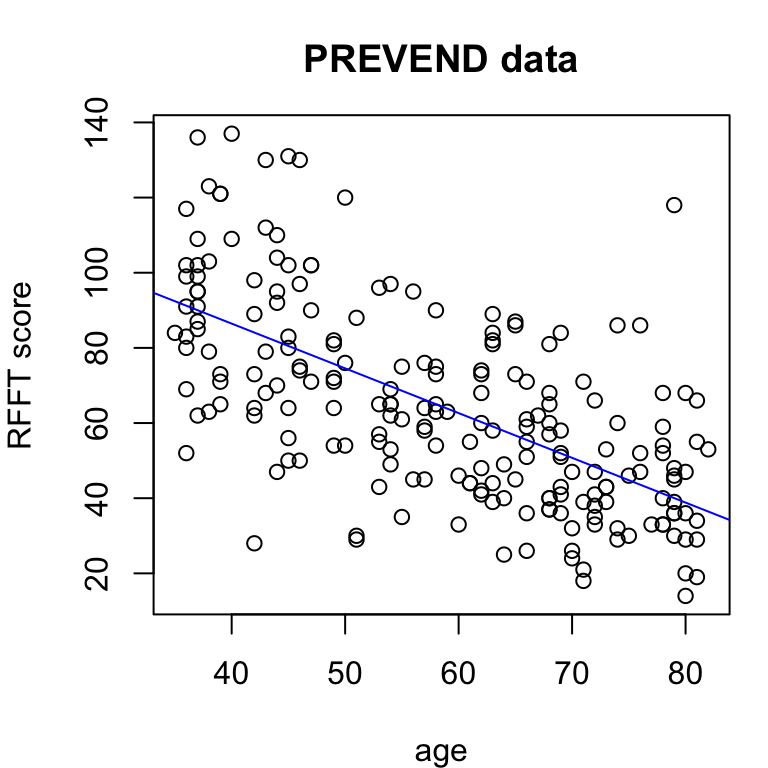
How much does RFFT decline with age?

Simple linear regression (SLR) model: $RFFT = β_{0} + β_{1} age + ϵ$

# least squares estimates
fit <- lm(formula = rfft ~ age, data = prevend)
fit


Call:
lm(formula = rfft ~ age, data = prevend)

Coefficients:
(Intercept)          age  
    134.098       -1.191

Interpretation:

With each additional year of age, mean RFFT score decreases by an estimated 1.191 points.

From last time

The residual standard deviation is an estimate of the unexplained variation in RFFT.

$\hat{σ} = \sqrt{\frac{1}{n - 2} \sum_{i} e_{i}^{2}}$

# compute residual sd
sigma(fit)

[1] 20.51788

More unexplained variation entails more sampling variability in the model fit.

Standard errors for the coefficients

Standard errors for the coefficients are:

$S E ({\hat{β}}_{0}) = \hat{σ} \sqrt{\frac{1}{n} + \frac{{\bar{x}}^{2}}{(n - 1) s_{x}^{2}}} and S E ({\hat{β}}_{1}) = \hat{σ} \sqrt{\frac{1}{(n - 1) s_{x}^{2}}}$

While you won’t need to know these formulae, do notice that:

more data $⟶$ less sampling variability
more spread in $x$ $⟶$ less sampling variability
more spread in $y$ about $x$ $⟶$ more sampling variability

Inference for the slope parameter

If the errors are symmetric and unimodal, then the sampling distribution of $T = \frac{{\hat{β}}_{1} - β_{1}}{S E (β_{1})}$ is well-approximated by a $t_{n - 2}$ model.

Significance test: ${\begin{cases} H_{0} : β_{1} = 0 \\ H_{A} : β_{1} \neq 0 \end{cases}$
Confidence interval: ${\hat{β}}_{1} \pm c \times S E ({\hat{β}}_{1})$

$P (T > | T_{obs} |) \approx 0$ : evidence of an association (true slope is not zero)
confidence interval using $t_{206}$ critical value: (-1.389, -0.992)

Inference for the intercept is analogous, but not very common.

Model summary

The model summary shows most quantities of interest, except CIs.

# model summary
summary(fit)


Call:
lm(formula = rfft ~ age, data = prevend)

Residuals:
    Min      1Q  Median      3Q     Max 
-56.085 -14.690  -2.937  12.744  77.975 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 134.0981     6.0701   22.09   <2e-16 ***
age          -1.1908     0.1007  -11.82   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 20.52 on 206 degrees of freedom
Multiple R-squared:  0.4043,    Adjusted R-squared:  0.4014 
F-statistic: 139.8 on 1 and 206 DF,  p-value: < 2.2e-16

${\hat{β}}_{0} = 134.10, {\hat{β}}_{1} = - 1.19, \hat{σ} = 20.52$
Age explains an estimated 40.43% of variation in RFFT.
With each year of age mean RFFT declines by an estimated 1.19 points (SE 0.10).
There is a significant association between age and mean RFFT score (T = -11.82 on 206 degrees of freedom, p < 0.0001).

Take a moment to locate the quantities that support the conclusions listed at right.

Confidence intervals

Confidence interval:

# ci for model parameters
confint(fit, level = 0.95)

                 2.5 %      97.5 %
(Intercept) 122.130647 146.0654574
age          -1.389341  -0.9922471

With 95% confidence, each additional year of age is associated with a decrease in mean RFFT score of between 0.99 and 1.39 points.

Since the intercept is not meaningful in this context, we don’t interpret that interval.

Prediction in SLR

Prediction is a matter of plugging in values to the estimated model equation.

For example, the predicted RFFT score for a 55-year old is:

$\hat{y} = 134.0981 - 1.1908 \times 55 = 68.604$

# model prediction for a 55 year old
predict(fit, newdata = data.frame(age = 55))

       1 
68.60439

Intervals for the mean

There are two possible ways to interpret model predictions:

The estimated mean RFFT score for 55-year-olds is 68.6
The predicted value of RFFT for a specific 55-year-old individual is 68.6

# model prediction for a 55 year old
predict(fit, newdata = data.frame(age = 55), 
        interval = 'confidence', 
        level = 0.95)

       fit     lwr      upr
1 68.60439 65.7101 71.49868

With 95% confidence, the mean RFFT score among 55-year-olds is estimated to be between 65.71 and 71.50 points.

Intervals for predicted values

There are two possible ways to interpret model predictions:

The estimated mean RFFT score for 55-year-olds is 68.6
The predicted value of RFFT for a specific 55-year-old individual is 68.6

# model prediction for a 55 year old
predict(fit, newdata = data.frame(age = 55), 
        interval = 'prediction', 
        level = 0.95)

       fit      lwr      upr
1 68.60439 28.04903 109.1598

With 95% confidence, the RFFT score for an individual 55 year old is estimated to be between 28.05 and 109.16 points.

Uncertainty bands

Pointwise intervals shown along the line provide a visual of the model uncertainty.

Why the difference? Individual observations are more variable than averages.

Kleiber’s law

fit <- lm(log.metab ~ log.mass, data = kleiber)
summary(fit)


Call:
lm(formula = log.metab ~ log.mass, data = kleiber)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.14216 -0.26466 -0.04889  0.25308  1.37616 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  5.63833    0.04709  119.73   <2e-16 ***
log.mass     0.73874    0.01462   50.53   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4572 on 93 degrees of freedom
Multiple R-squared:  0.9649,    Adjusted R-squared:  0.9645 
F-statistic:  2553 on 1 and 93 DF,  p-value: < 2.2e-16

${\hat{β}}_{0} = 5.638, {\hat{β}}_{1} = 0.739, \hat{σ} = 0.457$

There is a significant association between body mass and metabolism (p < 0.0001): body mass explains 96.49% of variation in metabolism; with 95% confidence, a unit increment in log mass is associated with an estimated increase in mean log metabolism between 0.7097 and 0.7678.

Kleiber’s law

How much energy do we consume on a daily basis?

Conversions:

110lb $\approx$ 50kg
180lb $\approx$ 80kg
1 kJ $\approx$ 0.239 kcal

# range of body mass
mass <- seq(50, 80)

# interval for mean log energy
pred <- predict(fit, 
                newdata = data.frame(log.mass = log(mass)), 
                interval = 'confidence')
# convert
estimates <- 0.239*exp(pred)

Using the SLR model, estimated resting energy consumption is:

$\hat{y} = 281 \times {mass}^{0.74}$

Left, prediction curve with 95% confidence interval.

Kleiber’s law

How much energy do you consume on a daily basis?

Conversions:

110lb $\approx$ 50kg
180lb $\approx$ 80kg
1 kJ $\approx$ 0.239 kcal

# range of body mass
mass <- seq(50, 80)

# interval for mean log energy
pred <- predict(fit, 
                newdata = data.frame(log.mass = log(mass)), 
                interval = 'prediction')
# convert
estimates <- 0.239*exp(pred)

Using the SLR model, estimated resting energy consumption is:

$\hat{y} = 281 \times {mass}^{0.74}$

Left, prediction curve with 95% prediction interval.

Hubble constant

The Hubble constant $H$ relates a galaxy’s relative distance and velocity as $H = \frac{v}{d}$ .

# fit SLR model without an intercept
fit <- lm(distance ~ velocity - 1, 
          data = hubble)

Least squares estimate of $β = \frac{1}{H}$ :

$\hat{β} = 0.0123$

90% CI for the age of the universe:

# interval for age of universe in bn yr
km.mpc <- 3.09e19
yr.sec <- 1/(60*60*24*365)
confint(fit, level = 0.9)*km.mpc*yr.sec/1e9

              5 %     95 %
velocity 10.98235 13.12108

With 90% confidence, the universe is estimated to be between 10.98 and 13.12 billion years old.